Final Report: Parallel Game Tree Evaluation
Nancy Xiao (nnx) and Jemmin Chang (jemminc)
Summary
We investigated how to best achieve speedup with a multi-core CPU in the task of game tree evaluation. From a baseline of sequential minimax, we implemented and optimized the runtime of parallel minimax and sequential and parallel alpha-beta pruning algorithms, testing them on Gomoku (generalized Tic-Tac-Toe) on the latedays cluster.
Our code is on GitHub.
Background
Overall, we specified the number of plies (depth of the game tree), trials and turns to run for the game. After running the game for the specified number of turns, each to the specified depth in the game tree, we recorded the output: time in seconds it took to complete those turns. Implementation-wise, we wanted a generalized version that could work with any solver algorithm and any two-player combinatorial game. As such, we created two interfaces: one for games and the other for various solvers.
- Game:
- Gomoku - A generalized version of Tic-Tac-Toe. It has two parameters: n and k. n represents the width and height of the board. k represents the number of same pieces in a row (diagonally, horizontally, or vertically) a player needs to win. We chose Gomoku because it has a high branching factor. For this game, there is low memory usage and simple state evaluation computation. The central region of the board requires more computation than the borders.
- <state, move>: The state keeps track of which player moves next (whose turn) and the state of the board.
- availableMoves(): Returns a vector of all possible moves based off the state. In this case, all the empty grid cells left.
- playMove(Move m): Plays the move specified
- undoMove(Move m): Undoes the move specified
- Etc.
- Solver Algorithms:
- Minimax Algorithm: finds the best next move in a game by minimizing the worst case scenario. It searches the game tree to the specified depth, calculating the value of each children based off a heuristic, and determines the best possible move. Minimax can be parallelized by computing the moves (child nodes) in parallel. See proposal below for diagram.
- Alpha-Beta Algorithm: similar to minimax algorithm in goal and purpose. The key difference is that it prunes away (does not compute or evaluate) the branches (moves) that are evidently worse by looking at the results of the previously computed branches. This algorithm is inherently sequential. We will be spending the bulk of our time parallelizing this well to achieve speedup.
- Principal Variation Splitting: The purpose of principal variation splitting is to start the parallel alpha-beta threads with a decent starting alpha-beta bound to yield more pruning. It does this by sequentially running the leftmost child to get starting alpha-beta bounds to evaluate the remaining children in parallel with. This approach assumes that the leftmost child is a decent (and hopefully very good) move. The better the leftmost child is as a move, the more it can prune away in the parallel run of the rest of the children. The sequential aspect is not that bad as the PVS algorithm is recursive, evaluating the remaining children of each level in parallel so our cores are never sitting idle.
Approach
First, we designed the interfaces in which we worked. This includes the game interface and the solver interface (for more details see the background section). From there, we implemented both the games and the solvers.
Initially, we wanted to implement chess as at each step, there are a lot of possible moves (and therefore a high branching factor) and would benefit from minimax and alphabeta pruning. We realized that it would be more worth our time to implement and improve upon the parallel solvers, especially the alpha-beta pruning algorithm, so we stopped implementing chess. However, we still needed to implement a game to test the solvers (baseline and improvements). We decided to implement Tic-Tac-Toe. Because there weren’t too many turns to simulate, we opted for a more generalized version of Tic-Tac-Toe (nxn board must get n in a row). However, that game tends to tie quickly and the range of values for possible moves is narrow, so we decided to implement othello, until we realized that othello also does not have a very high branching factor. Ultimately, we implemented Gomoku, an even more generalized version of Tic-Tac-Toe as one wins with k in a row on a nxn board. We also had to design a heuristic (evaluation function of a leaf node/move) to the best of our ability.
For the solvers, we started by implementing the baselines: sequential minimax, parallel minimax, sequential alphabeta and parallel alphabeta. For the first parallel solvers, we used OpenMP where each thread is statically assigned a chunk of the moves to evaluate. In this way, we achieved a 12x speedup (number of processors in a latedays cluster) from sequential to parallel minimax. However, we didn’t achieve such ideal speedup from sequential to parallel alpha beta pruning (only 5.8x speedup). (We also implemented alternative versions of each that either copied the game before playing a candidate move and evaluating its value, or just playing the move on the game, evaluating, then undoing it. The latter we supposed would reduce time spent copying arrays, but it turned out to make little difference, since the rest of the computation (evaluation heuristic) dominated.) Thinking that our parallel alpha-beta might have sub-optimal speedup because of contention over global variables (alpha, beta, best_score, best_move), we decided to implement another version of OpenMP parallel alpha-beta pruning that kept a thread-local version of all those variables and combined them at the end, as well as global and thread-local versions of parallel minimax. In this way, there would be less writes to the same chunk of memory. Upon testing, we saw that the global and local version of minimax were taking the same amount of time consistently and realized that there actually isn’t much contention, since the variables are updated relatively infrequently given the long tree evaluation computation that occurs between each potential update. We also noticed that the global alpha beta pruning solver was consistently faster than the local one. This is because the local version does not prune away as many branches as the global version does, since each thread obtains a worse thread-local alpha-beta bound in its course than it would if it shared a global one. See Figure 1.
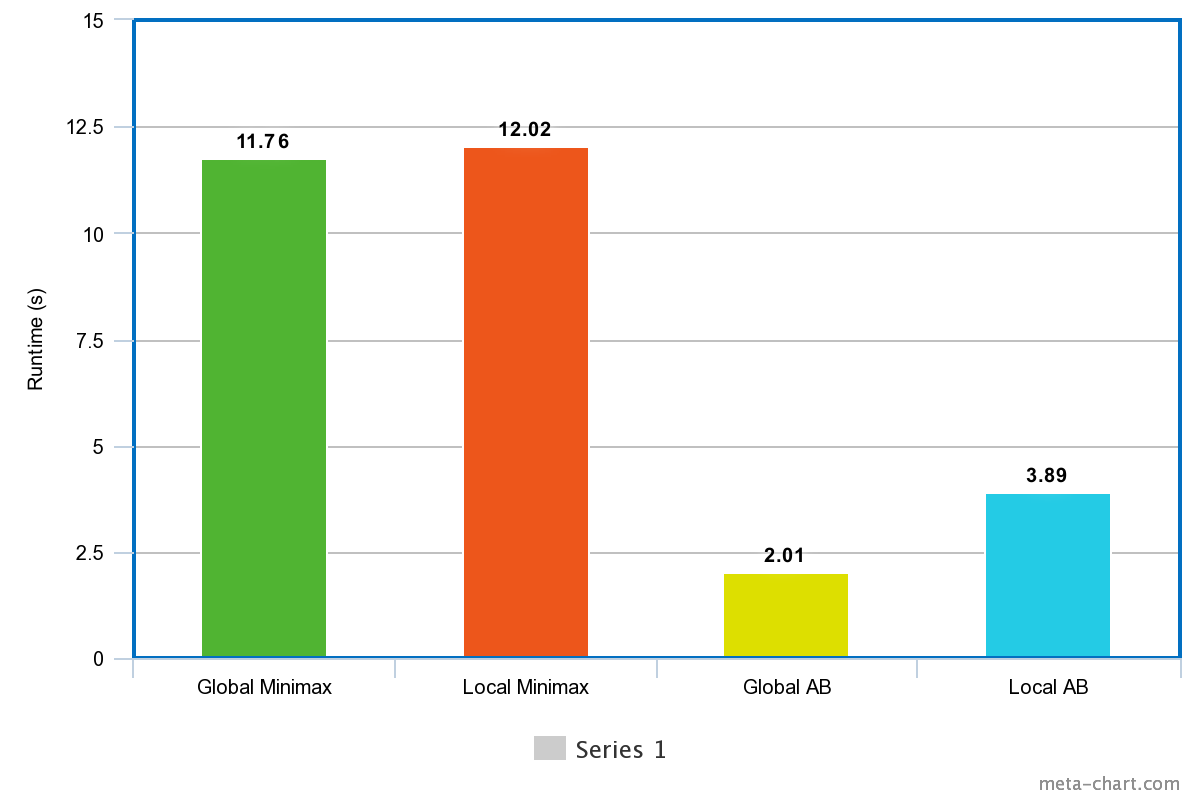
In order to further improve the parallelization and achieve greater speedup of alpha-beta pruning, we tried implementing principal variation splitting. We tried three methods of choosing the leftmost child (the move we hope to be fairly good as so to prune away more branches later): first move, random move, and best move (please see results below to understand the differences in outcome of the three methods).
Results
For all of our evaluation, we used a 15x15 Gomoku game with 5-in-a-row to win. We made 10 consecutive turns each searching to a depth of 3 in the game tree to find the best move according to minimax (correct pruning doesn’t change the final move chosen, modulo ties). We ran these evaluations for each different solving algorithm (sequential minimax, sequential alpha-beta, parallel alpha-beta, PVS, etc.) from each of two starting positions: an empty board (initial position) and an intermediate position (10 turns in). We measured wall clock time to complete the 10 turns. The goal was to minimize the ratio of parallel algorithm wall clock time to sequential algorithm wall clock time.
Our baselines are sequential minimax and sequential alpha-beta algorithms. For scale, it’s interesting to note that sequential alpha-beta runs 12x faster than sequential minimax due to pruning. Parallel minimax implemented with OpenMP achieved ~12x speedup over sequential, as expected from the 12 physical cores on latedays. Our basic parallel alpha-beta implemented with OpenMP achieved 5.8x speedup over sequential alpha-beta, roughly half of the ideal speedup. See Figure 2.
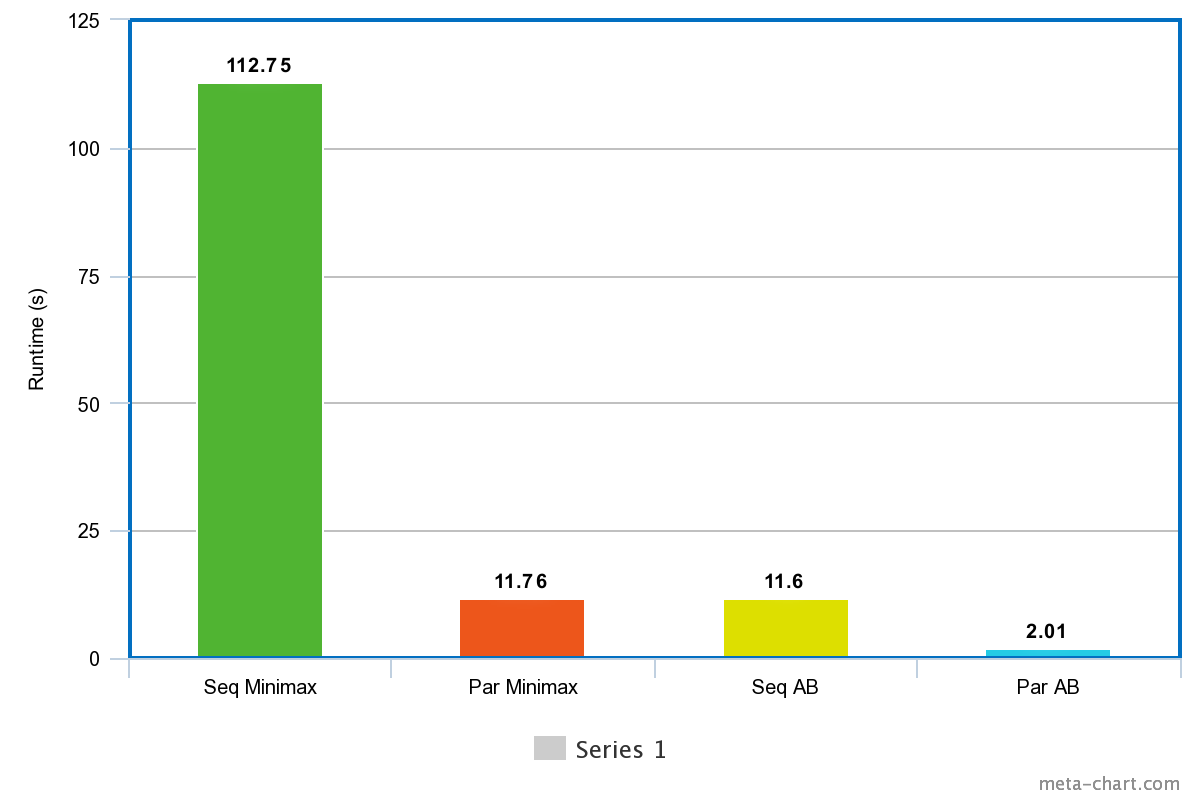
We implemented Principal Variation Splitting, an improvement on our simple parallel alpha-beta, to increase its pruning and reduce computation. The success of PVS depended on how the principal variation (the move evaluated sequentially to obtain an initial alpha-beta bound) was selected; the better the PV move, the better bound it yields, leading to more pruning. Choosing the first available move as PV demonstrated performance worse than the basic parallel alpha-beta, probably due to the extra initial sequential work of PVS. The first move does not yield a useful bound at the stages of the game we evaluated on because it is in the corner of the board, too far from existing placed pieces. Choosing a random move as PV performed better, balancing out the overhead of PVS to get equal performance with our basic parallel alpha-beta, but a randomly chosen move is still most likely to be bad. Finally, using the leaf node heuristic to evaluate moves and select the best one according to its score to use as PV yielded runtime about 20% shorter than the basic parallel alpha-beta, representing a final best speedup of 7.2x faster runtime than the sequential alpha-beta algorithm. The results shown below are all when starting from an initial state of the board. From the intermediate state, all of our PVS algorithms yielded performance equal to or worse than the basic parallel alpha-beta, especially the heuristic selector. We hypothesize that the simple heuristic function we used gives an inadequate estimate of the value of intermediate positions, although it works reasonably well towards the initial state of the game. See Figure 3.
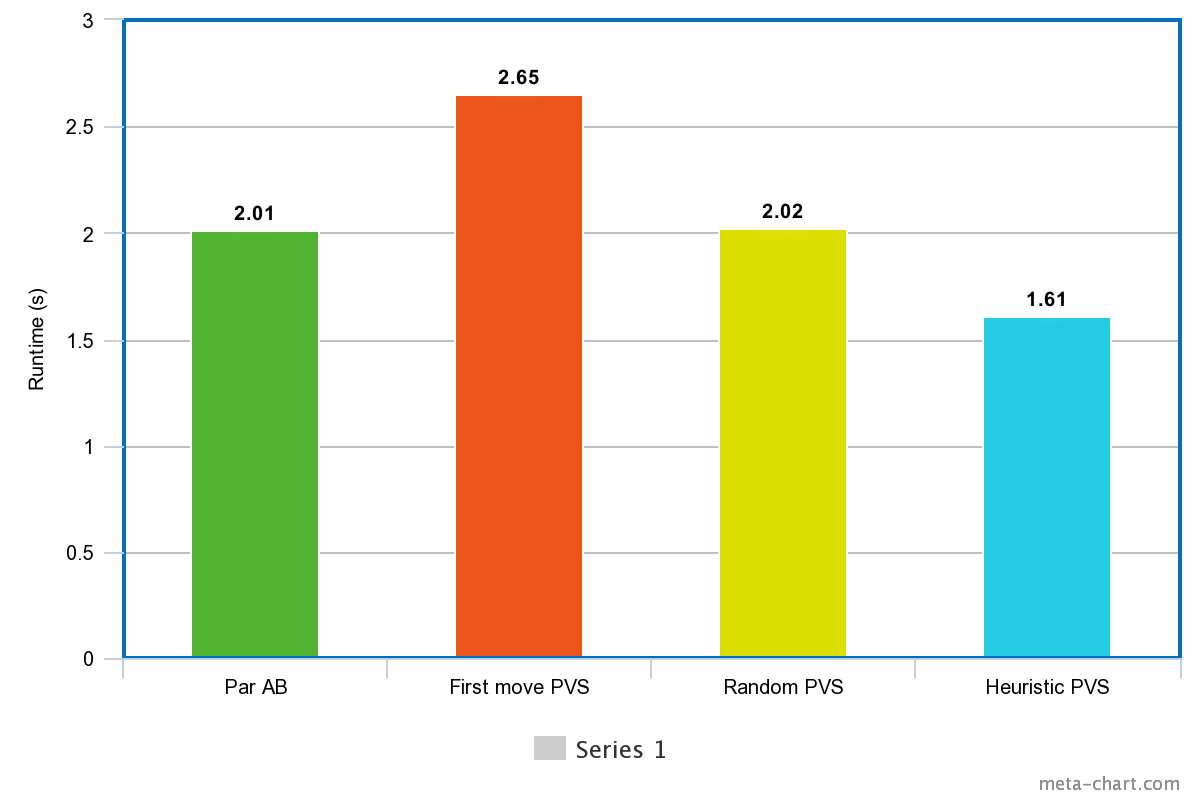
We are still far short of the ideal 12x speedup from our 12 physical cores. We hypothesize that this is due to workload imbalance between the static chunks assigned to each core, since by nature of pruning some of them will find better alpha-beta bounds earlier and prune a lot more computation, finishing earlier than others and waiting. The workload imbalance is exacerbated by the use of PVS, since starting with a better bound enables earlier and more variable pruning, and the amount of computation pruned is highly dependent on the static region of the board assigned to the core (since moves were generated in row-major order), and the center of the board usually contains the better moves. We did not have time to complete extensive analysis to measure workload imbalance, but examining thread timings a bit suggested that occasionally some threads do finish orders of magnitude earlier than others. A dynamic work scheduling or stealing algorithm such as Dynamic Tree Splitting (DTS) as suggested in our initial proposal would help alleviate this inefficiency.
References
- To briefly understand the various algorithms related to parallel search
- To better understand Principal Variation Splitting
- Wikipedia on minimax
- Wikipedia on alpha-beta
List of work by each student
Equal work was performed by both project members.
Checkpoint: Parallel Game Tree Evaluation
Nancy Xiao (nnx) and Jemmin Chang (jemminc)
Progress
Summary of work completed
- Learned some make, set up Makefile; set up simple test harness with timing
- Designed modular interfaces for games and solvers so they can be easily plugged together
- Implemented tic-tac-toe to have a simple game to test solvers on
- Implemented sequential minimax solver (one of our baselines)
- Started implementing chess game
Summary of excuses for being behind schedule
- Ramping up with C++ took longer than expected, particularly designing clean modular game and solver interfaces using templates
- Carnival was funner than expected (did less work than planned)
- Overall, haven’t run into any major issues yet; just need to put in time to code
Updated Goals and Deliverables
Our goals have not changed. We still plan on finding the optimal algorithm to parallelize the minimax algorithm by parallelizing minimax, implementing sequential and parallel alpha-beta pruning, and finally improving the parallel alpha-beta pruning algorithm by implementing principal variation splitting (PVS). We were hoping to have enough time to implement Dynamic Tree Split. However, we aren’t too hopeful as it is a tricky algorithm and the next few weeks are looking a bit rough. We might be able to try simpler improvements such as iterative deepening or jamboree. For the demo we still plan to present speedup graphs (and we'll try to compute win rates from pitting various solvers against each other under time constraints, because it’s cool, but if we don't get to that it's not our main metric anyway.)
Updated Schedule for Remaining Time
| Dates | jemminc | nnx |
|---|---|---|
| 4/26-4/28 | Start implementing parallel minimax with OpenMP | Implement the overall chess game structure |
| 4/29-5/1 | Finish parallel minimax | Implement getting all possible moves for chess (finish chess) |
| 5/2-5/4 |
Implement alpha-beta pruning for reference time
Read up on PVS |
Implement alpha-beta pruning for reference time
Read up on PVS |
| 5/5-5/7 | Start parallelizing alpha-beta pruning using PVS | Finish implementing alpha-beta pruning Implement naive parallel alpha-beta pruning (OpenMP) |
| 5/8-5/10 | Finish parallelizing alpha-beta pruning using PVS | Improve upon PVS using either iterative deepening or dynamic tree split |
| 5/11-5/12 |
Report
Finish Improving PVS |
Report
Finish Improving PVS |
Proposal: Parallel Game Tree Evaluation
Nancy Xiao (nnx) and Jemmin Chang (jemminc)
Summary
We will investigate how to best achieve speedup with a multi-core CPU in the task of game tree evaluation. From a baseline of sequential minimax, we will implement and optimize speedup of parallel minimax and a few sequential and parallel alpha-beta pruning algorithms (Principal Variation Splitting, iterative deepening, Dynamic Tree Splitting), testing it on various games such as Chess on the latedays cluster.
Background
The minimax algorithm is used to find the best next move in a game by minimizing the worst case scenario. Parallelizing minimax is fairly intuitive as it involves spawning threads for each node (next possible move) and running those in parallel.

Unfortunately, a lot of the speedup from parallelizing the algorithm is unnecessary as many branches could have been pruned, e.g. with the alpha-beta pruning algorithm. Alpha-beta pruning is an algorithm that speeds up the minimax search on a game decision tree by not fully evaluating branches that cannot be the best choice given the results already achieved in previously evaluated choices.

To parallelize the alpha-beta pruning algorithm, we will implement the Principal Variation Splitting and Dynamic Tree Splitting algorithms. The Principal Variation Splitting (PVS) algorithm represents each node on the decision tree as a thread. In order words, each move is a thread. In order to set the alpha and beta values, the PVS algorithm runs the first child sequentially. Then using the alpha-beta bounds obtained, it runs the other children nodes in parallel with those values. Sometimes, for ideal alpha beta values, there might not be a need to run the other children. This reduces contention of alpha beta global variables, allowing for more efficient parallel execution. Unfortunately, since some moves will be pruned, some threads will be idle while they wait for other children threads to finish, leading to load imbalance. There are some ways to remedy this, including Enhanced PVS, iterative deepening, and Dynamic Tree Splitting. Iterative deepening reorders the nodes at each iteration according to a shallower evaluation such that the first node the PVS would run sequentially would ideally be the best value and therefore reduce the number of parallel runs. Dynamic Tree Splitting is much like PVS with work-stealing as each node reports its state so that free threads can look at these states and decide whether it can help that node finish its work. It does this by splitting a block. If the free thread does decide to join in on the work, the current state of that heavy-work node will be added into shared memory and the two threads will split the block.
Overall, we will be parallelizing across nodes (each a thread) for each level, pruning off branches that are not very useful, reorganizing work, and redistributing/splitting up work for better load balance.
The Challenge
Overall, the minimax algorithm is compute-intensive and needs little memory bandwidth. Parallelizing alpha-beta pruning is the main challenge of this project, because pruning inherently works because of its sequential dependencies -- you avoid doing work by knowing that it is unnecessary given the previous work you’ve done. Naively trying to globally share and update the alpha-beta values would lead to extreme contention which could actually result in slowdown compared to sequential alpha-beta. To combat this, we will implement the Principal Variation Splitting (PVS) algorithm as described in the background section. Unfortunately, PVS is susceptible to severe load imbalance as some threads are left idle when their branch gets pruned. Dynamic Tree Splitting (as described in the background section), a hard-to-implement algorithm, helps to overcome this problem.
Resources
We will probably use the latedays cluster and start from scratch. We will refer to these papers/slides:
Goals and Deliverables
Plan to achieve:
- Implement simple, low-memory representation of chess game logic and simple game state evaluation heuristic for testing purposes
- Implement standard, sequential minimax as a baseline Parallelize minimax with multi-threading on CPU; goal: achieve linear speedup with number of cores
- Implement sequential alpha-beta pruning; measure speedup against sequential and parallel minimax (we expect that sequential alpha-beta pruning will provide better speedup than parallel minimax)
- Implement parallel alpha-beta pruning with PVS; goal: 0.5p speedup with p cores (note: not really sure whether this is too low or high; we know PVS will not get linear speedup, but have to look at papers to see what is a reasonable expectation)
Hope to achieve:
- Implement iterative deepening to improve the speedup of PVS alpha-beta (hard to set a speedup goal, no precedent)
- Implement DTS to improve the speedup of PVS alpha-beta to linear compared to sequential alpha-beta
How we will demonstrate:
To demonstrate our project, we will show the speedup graphs of all the algorithms we implement. The ultimate baseline for all will be the sequential minimax, but the various parallel alpha-beta techniques compared to sequential alpha-beta will be of particular interest as well. For fun, we will also present statistics on the differences in win rate of the different algorithms (with a fixed time limit per turn), although the main goal is to optimize the parallel algorithm runtime and we know this will not necessarily translate directly to linear improvements in win rate.
Platform Choice
We will be focusing on achieving speedup from use of a multi-core CPU. Since pruning algorithms naturally have strong sequential dependencies, very wide parallelism (e.g. SIMD execution on GPU) is unlikely to yield very good speedup. We plan to code in C++, and we will probably use OpenMP or Cilk as Cilk is good with divide and conquer parallel algorithms.
Schedule
- Week of 04/10/2017
- Implement + measure sequential minimax
- Implement + measure parallel minimax
- Start implementing sequential alpha-beta pruning
- Start implementing chess logic
- Week of 04/17/2017
- Finish + measure sequential alpha-beta pruning
- Start parallelizing alpha-beta with PVS
- Finish implementing chess logic
- Checkpoint
- Week of 04/24/2017
- Finish parallelizing alpha-beta with PVS
- (Study for 418 Exam 2)
- Week of 05/01/2017
- Improve upon PVS speedup with iterative deepening
- Start parallelizing alpha-beta with DTS
- Week of 05/08/2017
- Finish parallelizing alpha-beta with DTS
- Final report